В равнобедренном треугольнике основание равно 4, а боковая сторона равна 8. Найти квадрат...

Ответ: 15.

Пошаговое объяснение:

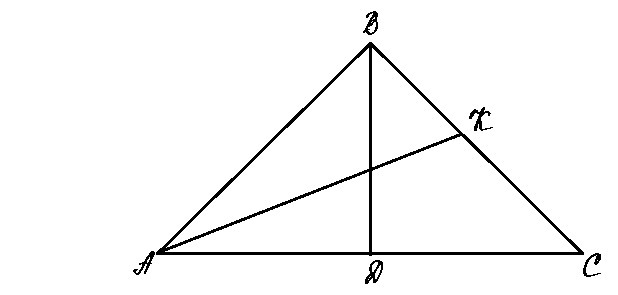
АВ = ВС = 8, АС = 4. Высота, проведенная из вершины В к стороне основания АС, делит основание пополам, т.е. AD=CD=AC/2=2

Найдем высоту BD по теореме Пифагора из прямоугольного треугольника ADB.

$BD=\sqrt{AB^2-AD^2}=\sqrt{8^2-2^2}=2\sqrt{15}$

Площадь треугольника $S=\dfrac{AC\cdot BD}{2}$ , с другой стороны $S =\dfrac{BC\cdot AK}{2}$ . Осталось приравнять площади и найти высоту, опущенной на боковую сторону

$AC\cdot BD=BC\cdot AK\\ \\ AK=\dfrac{AC\cdot BD}{BC}=\dfrac{4\cdot2\sqrt{15}}{8}=\sqrt{15}$

Квадрат высоты, опущенной на боковую сторону: $AK^2=15$