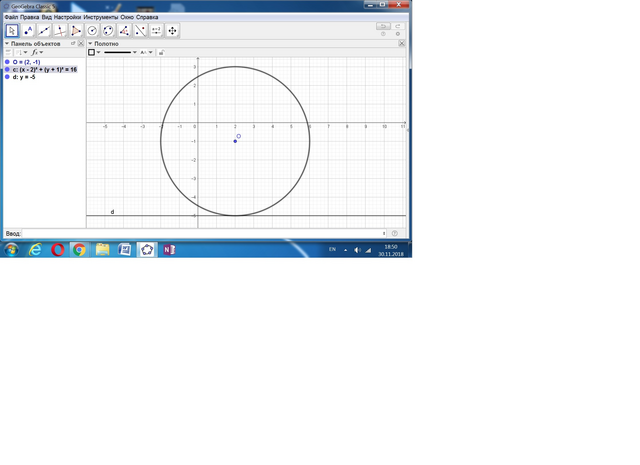
Проанализируем исходные данные.
Дан эллипс с центром в точке (2:-1) и малой осью, равной 4.
Одна из директрис задана уравнением y+5=0, что равносильно у = -5.
Тогда расстояние от центра до директрисы равно |-5 - (-1)| = 4.
Рассмотрим точку эллипса на малой оси. Она удалена от центра на 4 и от директрисы на 4 единицы (так как малая ось параллельна директрисе).
Так как все точки параболы равноудалены от директрисы и фокуса, то получается, что фокус параболы находится в её центре.
Это говорит о том, что мы имеем не эллипс, а окружность радиуса 4.
Её уравнение: (х - 2)² + (у + 1)² = 4².