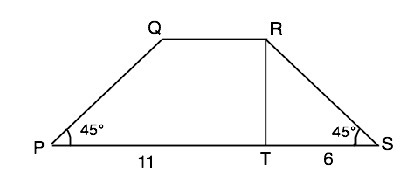
В равнобедренной трапеции PQRS угол Р равен 45°, RT - высота трапеции, РТ=11 см, ТS=6 см. Найдите площадь трапеции.
Площадь трапеции равна произведению ее высоты на полусумму оснований. S=h•(a+b):2. Высота равнобедренной трапеции, опущенная из вершины тупого угла, делит основание на отрезки, больший из которых равен полусумме оснований, меньший – их полуразности. Следовательно, (QR+PS):2=РТ=11 см. Высота RT - катет прямоугольного треугольника с углом, равным 45°. RT=TS•tg45°=6•1=6 см. ⇒ S(PQRS)=6•11=66 см²