1. Высота — AH (знак квадрат обозначает, что отрезок проведен под прямым углом), BC — медиана (сторона, к которой она проведена делится на равные части, они обозначены кружочками), MT — биссектриса (делит угол пополам, образуя при этом два равных — душки одинаковые)
2. Угол BAC = углу №1 = 64 (они вертикальные и равны). Треугольник равнобедренный, значит углы при основании равны, а следовательно — угол ACB = 64, значит угол №2 = 180 - угол ACB = 180 - 64 = 116 (как смежные)
3. Пусть основание - x, тогда две боковые стороны по 4x. В сумме образуют периметр: x+4x+4x=9x=36. Следовательно, x=4 см - основание. А две боковые стороны по 4*4=16 см
4. Угол CPO = угол PCT / 4 = 60 / 4 = 15. Угол PCT + угол CPO = угол OPT; 60+15=75 - угол OPT, но и угол OTP = 75, т.к. треугольник OPT — равнобедренный. Значит, угол POT = 180 - угол OPT - угол OTP = 180 - 75 - 75 = 30.
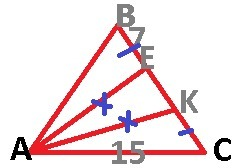
5. Начертим. Докажем равенство треугольников ABE и AKC, они равны по двум сторонам и углу между ними (AK=AE - усл., KC=BE=7 - усл. и угол AKC = углу AEB, т.к. углы при основании в треугольнике AFK равны.). Следовательно, AB=AC=15. Пусть сторона EK - x, тогда периметр: 15+15+7+7+x=50. Отсюда находим x, он равен 6. EK=6