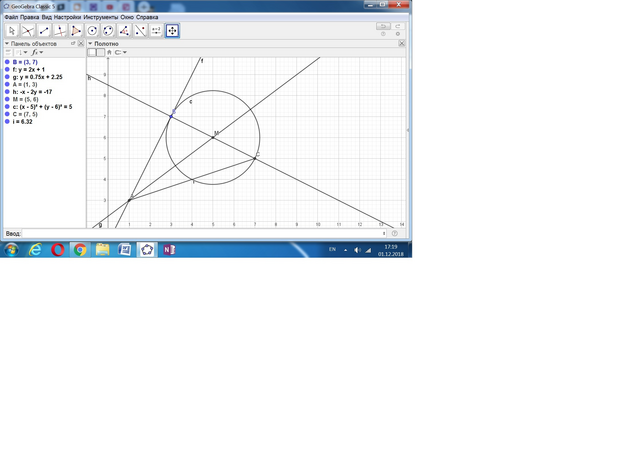
Рисунок не соответствует условию. Если подставить координаты точки В(3; 7) в уравнение высоты 2х - у + 1 = , то получим тождество:
2*3 - 7 + 1 = 0. Значит, точка В лежит на прямой 2х - у + 1, а прямая АВ - это катет прямоугольного треугольника.
Уравнение АВ: у = 2х + 1.
Уравнение ВС: у = -1/( 2)х + в. Поставим В(3; 7). 7 = (-1/2)*3 + в.
Отсюда в = 7 + (3/2) = 17/2. Тогда ВС: (-1/2)х + (17/2).
Находим координаты точки М (основание медианы) как точка пересечение ВС и АМ: (-1/2)х + (17/2) = (3/4)х + (9/4). (5/4)х = 25/4.
х (М) = 25/5 = 5. у(М) = (3/4)*5 + (9/4) = 24/4 = 6.
Точка М: (5; 6).
Теперь находим координаты точки С как симметричной точке В относительно точки М.
х(С) = 2х(М) - х(В) = 10 - 3 = 7.
у(С) - 2у(М) - у(В) = 12 -7 = 5.
Ответ: С(7; 5).