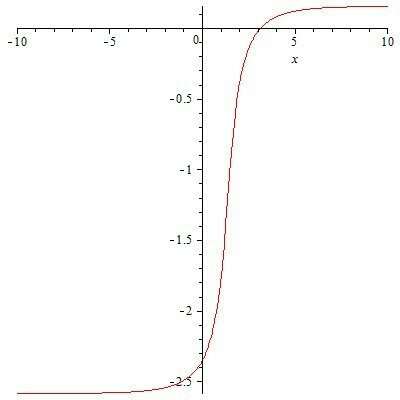
Известно, что если функция f(x) непрерывна на отрезке [a,b] и на его концах принимает значения разных знаков, на этом отрезке найдется такая точка , в которой значение функции равно нулю (теорема Коши).
Следовательно, наша задача - всего лишь проверить знаки значений заданной функции в точках a и b.
Увы, но Delphi у меня нет (как и всех почти, наверно), поэтому вот...
PascalABC.NET 3.4.2, сборка 1881 от 19.11.2018
Внимание! Если программа не работает, обновите версию!
begin
var (p, a, b) := ReadReal3('Введите p, a, b:');
var fx: real-> real := x -> ArcTan(2 ** x - Abs(p)) - Sqrt(2);
(fx(a) * fx(b) <= 0).Println</p>
end.
Пример
Введите p, a, b: 2.35 1 3.2
True
В данном случае нам повезло: корень у функции единственный. А вот если их на заданном отрезке попадатеся четное число, такое решение не годится. Более того, не существует универсального аналитического метода, который позволил бы для совершенно любой функции определить, единственный ли корень на заданном интервале и есть ли он там вообще.