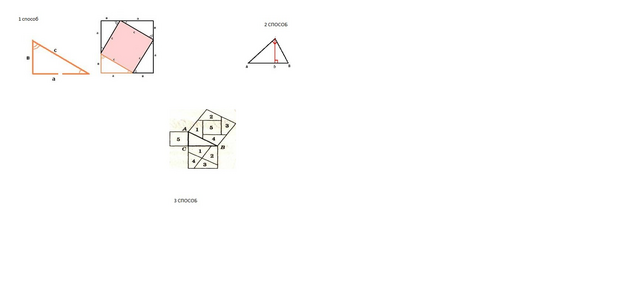
1.Пользуясь свойствами площадей многоугольников, установим замечательное соотношение между гипотенузой и катетами прямоугольного треугольника.
Доказательство.
Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с .Докажем, что с²=а²+в².
Доказательство.
Достроим треугольник до квадрата со стороной а + в . Площадь S этого квадрата равна (а + в)² . С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна ½ав , и квадрата со стороной с, поэтому S= 4 * ½ав + с² =2ав + с².
доказательство закончено.
2.
После изучения темы «Подобные треугольники» я выяснила, что можно применить подобие треугольников к доказательству теоремы Пифагора. А именно, я воспользовалась утверждением о том, что катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.
Рассмотрим прямоугольный треугольник с прямым углом С, СD– высота . Докажем, что АС² +СВ² = АВ².
Доказательство.
На основании утверждения о катете прямоугольного треугольника:
АС = , СВ = .
Возведем в квадрат и сложим полученные равенства:
АС² = АВ * АD, СВ² = АВ * DВ;
АС² + СВ² = АВ * ( АD + DВ), где АD+DB=AB, тогда
АС² + СВ² = АВ * АВ,
АС² + СВ² = АВ².
Доказательство закончено.
3.
Данное доказательство основано на разрезании квадратов, построенных на катетах , и укладывании полученных частей на квадрате, построенном на гипотенузе.