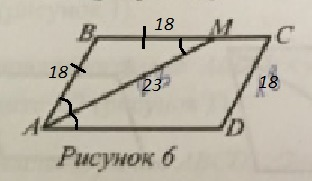
АВСД - параллелограмм, АМ - биссектриса ⇒ ∠ВАМ=∠МАД.
Так как у параллелограмма противоположные стороны равны, то СД=АВ=18 см. Так как у параллелограмма противоположные стороны ещё и параллельны, то ВС║АД ⇒ имеем две параллельные прямые и секущую АМ ⇒ внутренние накрест лежащие углы равны: ∠МАД=∠ВМА ⇒ ∠ВАМ=∠ВМА ⇒ ΔАВМ - равнобедренный ⇒ АВ=ВМ .
Но АВ=СД=18 см , тогда ВМ=18 см.
Периметр ΔАВМ равен Р=18+18+23=59 (см)