Неизвестные цифры обозначим буквами и запишем задачу в виде:
4АВС - АВС4 = 1071.
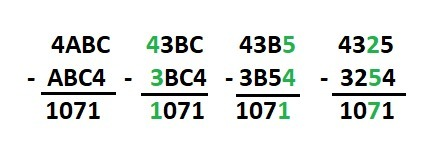
На рисунке в приложении решение "в столбик".
А = 4 -1 = 3 и С = 4 + 1 = 5 и В = 7 + С = 7 + 5 = 12 - 10 = 2.
Получили число 4325 и сумма его цифр:
4+3+2+5 = 14 и еще раз суммируем: 1 + 4 = 5.
ОТВЕТ: Сумма цифр - 5.