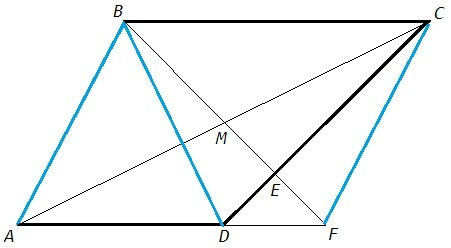
CF||AB, ABCF - параллелограмм.
AC, BF - диагонали ABCF. Диагонали параллелограмма точкой пересечения делятся пополам. M - середина AC => M∈BF, E∈BF.
CF=AB (противоположные стороны параллелограмма) => CF=BD, BDFC - равнобедренная трапеция.
BF, CD - диагонали BDFC. Диагонали равнобедренной трапеции образуют на основаниях равнобедренные треугольники (∠BCF=∠CBD, CF=BD, BC- общая => △BCF=△CBD, ∠CBF=∠BCD). BE=CE.