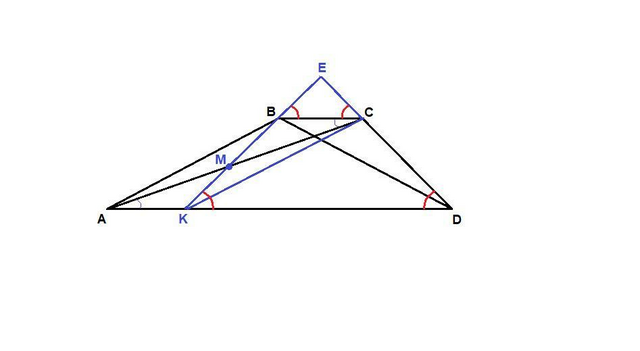
В трапеции ABCD боковая сторона AB равна диагонали BD. Точка M - середина диагонали AC. Прямая BM пересекает прямую CD в точке E. Докажите, что BE = CE.
Объяснение:
К - точка пересечения прямой ВМ с основанием AD.
Рассмотрим треугольники АМК и СМВ:
АМ = МС по условию,
∠АМК = ∠СМВ как вертикальные,
∠МАК = ∠МСВ как накрест лежащие при пересечении параллельных прямых АК и ВС секущей АС, ⇒
ΔАМК = ΔСМВ по стороне и двум прилежащим к ней углам.
Следовательно, АК = ВС.
Если в четырехугольнике две противолежащие стороны равны и параллельны, то это параллелограмм.
Значит, АВСК параллелограмм. ⇒ СК = АВ.
АВ = BD по условию, ⇒ СК = BD.
В трапеции KBCD диагонали равны, значит она равнобедренная.
Тогда ∠BKD = ∠CDK.
∠ЕВС = ∠BKD и ∠ЕСВ = ∠CDK как накрест лежащие при пересечении параллельных прямых KD и ВС секущими EК и ED соответственно, ⇒
∠EBC = ∠ECB.
Из этого следует, что треугольник ЕВС равнобедренный и
ВЕ = СЕ.