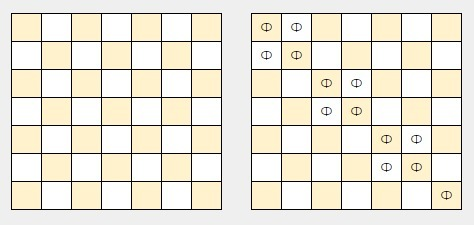
Раскрасим доску шахматной раскраской. Заметим, что между любыми закрашенными клетками в одном столбце (одной строке) расстояние нечётное, поэтому в каждом столбце (строке) может стоять не более одной фишки на закрашенной клетке и одной фишки на незакрашенной.
Обратим внимание на 4 столбца с нечетными номерами. Незакрашенные клетки в них входят только в 3 строки, поэтому в этих 4 столбцах может быть не более 3 фишек на незакрашенных местах и 4 фишек на закрашенных. В каждом из оставшихся столбцов можно поставить не более 2 фишек, поэтому всего фишек не более 13.
Пример, как поставить 13 фишек, на рисунке.