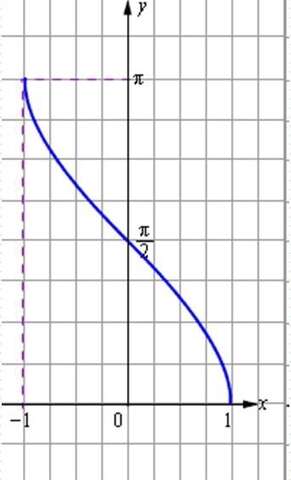
Sin (arccos(0.25)) Обясните пожалуйста очень подробно... :)

sin( arccosx ) = ?

Для начала вспомним, что такое arccosx.

Арккосинусом числа х называется такой угол Альфа ( а ) в пределах [ 0 ; п ], косинус которого равен х.

cosa = x , x принадлежит [ - 1 ; 1 ]

sin( arccosx ) = sina = $\sqrt{1 - (cosx)^{2}} = \sqrt{1 - x^{2}}$

Основное тригонометрическое тождество:

$(sinx)^{2} + ( cosx )^{2} = 1\\(sinx)^{2} = 1 - ( cosx )^{2} \\sinx = + - \sqrt{1 - ( cosx ) ^{2}}$

Заметьте, что перед квадратным арифметическим корнем стоит знак "+" , а не " + - ". В виду того что угол а принадлежит [ 0 ; п ], где синус положительный

______________________________

$sin(arccos \frac{1}{4} ) = \sqrt{1 - { (\frac{1}{4} )}^{2} } = \sqrt{1 - \frac{1}{16} } = \\ = \sqrt{ \frac{15}{16} } = \frac{ \sqrt{15} }{4} \\$

ОТВЕТ: $\sqrt{15} / 4$