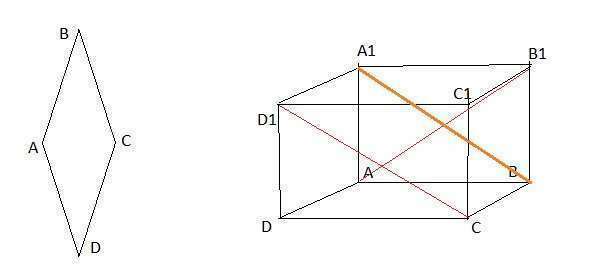
Угол между этими прямыми будет равен углу между прямыми АВ1 и ВА1
АВВ1А1 ---прямоугольник (т.к. призма прямая),
прямые АВ1 и ВА1 ---его диагонали
найдем сторону АВ
диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам... из прямоугольного треугольника по т.Пифагора
АВ^2 = 3^2 + 6^2 = 45
из треугольника ABB1 найдем АВ1 по т.Пифагора
AB1^2 = 45 + (V15)^2 = 60
AB1 = V60 = 2V15
диагонали прямоугольника равны и точкой пересечения делятся пополам,
т.е. образуют равнобедренный треугольник с основанием, равным V15 и боковыми сторонами, равными по половине диагонали = V15...
т.е. равнобедренный треугольник оказался равносторонним и угол даже искать не придется... он равен 60 градусов...