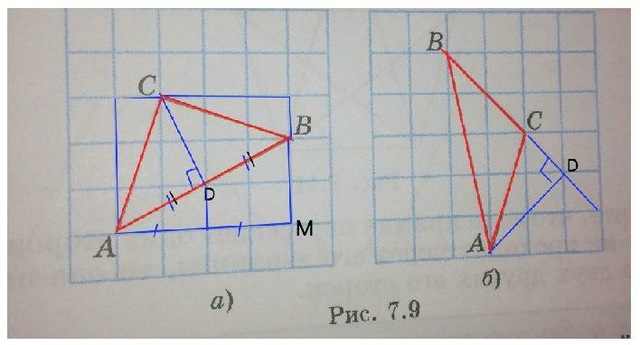
Объяснение: Все нижеописанное легко можно проделать мысленно, без дополнительных построений.
а) Обратим внимание на то, что АС=ВС ( прямоугольные треугольники по бокам от них равны по двум катетам). следовательно, их гипотенузы равны, поэтому ∆ АСВ - равнобедренный, и высота CD будет его медианой. Чтобы точно найти середину АВ, «пристроим» к ней как к гипотенузе прямоугольный треугольник АВМ. На катете АМ отметим середину и проведем от нее до пересечения с АВ перпендикуляр ( по клеткам). Он будет средней линией ∆ АВМ и разделит АВ пополам в точке D. Отрезок СD - медиана и высота равнобедренного ∆ АСВ.
б) В ∆ АВС сторона ВС проходит по диагоналям квадратных клеток. Продлим ВС на две клетки. Из т.А проведем по диагоналям квадратных клеток прямую, которая пересечет прямую ВС в т.D. Угол ВDА прямой, т.к. состоит из половин прямых углов квадратных клеток. => АD - высота ∆ АВС.