Геометрия. В плоскости треугольника АВС найти точку К, ближайшую к точке М. ДАЮ 30 БАЛЛОВ

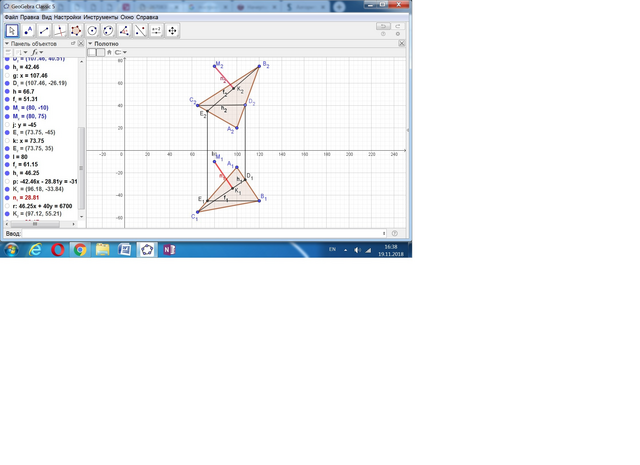
1. Для того чтобы построить перпендикуляр к плоскости Р( АВС) через точку М, необходимо сначала построить любую горизонталь в данной плоскости Р( АВС) – h (h1h2).

2. Строим фронталь в плоскости Р( АВС) – f ( f1f2).

3. Строим перпендикуляр n к плоскости Р( АВС). Для этого через точку М2 проводим n2, перпендикулярно f2, а через М1 проводим n1, перпендикулярно h1.

n (n1n2) Р (АВС), так как

n1h1; h1 P1 ( А1В1С1)

n2f2; f2 P2 (А2В2С2).

Более точно точку пересечения перпендикуляра из точки М на плоскость АВС можно найти аналитическим способом. По координатам точек А, В и С уравнение плоскости треугольника АВС находим: 64x + 93y - 74z - 6315 = 0. Направляющий вектор перпендикуляра равен нормальному вектора плоскости N = (64; 93; -74). Уравнение перпендикуляра: (x-80)/64=(y-10)/93=(z-75)/(-74) приравняем лямбда (L). Тогда параметрическое уравнение x=64L+80; y=93L+10; z=-74L+75.