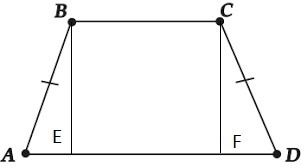
Опустим из вершин В и С две высоты - ВЕ и СF. Тогда ВС=EF. Так как трапеция - равнобедренная, то углы при основаниях равны.
∠А=∠D, ∠ABE=∠DCF AB=CD, то ΔABE=ΔDCF по второму признаку, то AE=FD=(14-8)/2=3 дм
По теореме Пифагора АB = √(BE²+AE²)=√(16+9)=5дм