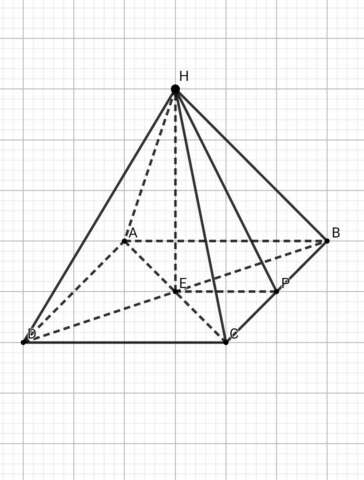
Апофема правильной четырёхугольной пирамиды равна 10 см, а радиус окружности, вписанной в основание пирамиды - 6 см. Чему равна площадь её боковой поверхности?
РЕШЕНИЕ:
• Апофема - это высота боковой грани правильной пирамиды, проведённая из её вершины => НР = 10 см
• В основании правильной четырёхугольной пирамиды лежит квадрат АВСD. Диаметр вписанной окружности в квадрат равен стороне квадрата => ВС = 2R = 2 • 6 = 12 см
• Площадь боковой поверхности правильной пирамиды вычисляется по формуле:
S бок. = ( 1/2 ) • P abcd • HP = ( 1/2 ) • 12 • 4 • 10 = 240 cм^2
Или можно найти площадь одной грани данной пирамиды и увеличить его в 4 раза, так как боковые грани правильной пирамиды равны
ОТВЕТ: 240