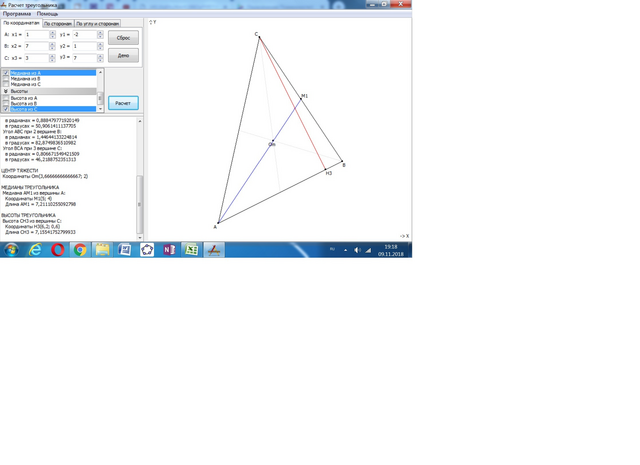
а) Уравнение стороны АВ:
Х-Ха У-Уа
______ = ______
Хв-Ха Ув-Уа
(х -1)/(7 - 1) = (у + 2)/(1 - (-2),
(х -1)/6 = (у + 2)/3 можно сократить на 3: (х -1)/2 = (у + 2)/1
в общем виде х - 2у - 5 = 0,
в виде с угловым коэффициентом у = (1/2)х - (5/2).
б) Уравнение высоты CH.
Угловой коэффициент к(СН) = -1/к(АВ) = -1/(1/2) = -2.
Уравнение СН имеет вид у = -2х + в.
Для определения параметра в подставим коэффициенты точки С, через которую проходит прямая.
7 = -2*3 + в,
в = 7 + 6 = 13.
СН: у = -2х + 13.
в) Уравнение медианы AM.
Точка М - середина ВС. М((7+3)/2=5; 1+7)/2=4) = (5; 4).
Уравнение АМ: (х - 5)/4 = (у + 2)/6
3х - 2у - 7 = 0.
у =(3/2)х - (7/2).
г) Точка N пересечения медианы AM и высоты CH.
Приравниваем уравнения медианы AM и высоты CH.
(3/2)х - (7/2) = -2х + 13.
3,5х = 16,5
х = 16,5/3,5 = 33/7.
у = -2*(33/7) + 13 = 25/7.
Точка пе- Х =4,714285714
ресечения У =3,571428571
.
д) Уравнение прямой, проходящей через вершину C параллельно стороне AB
.
у = (1/2)х + в.
Подставим координаты точки С: 7 = (1/2)*3 + в, в = 7 - 1,5 = 5,5.
Ответ: у = (1/2)х + 5,5.