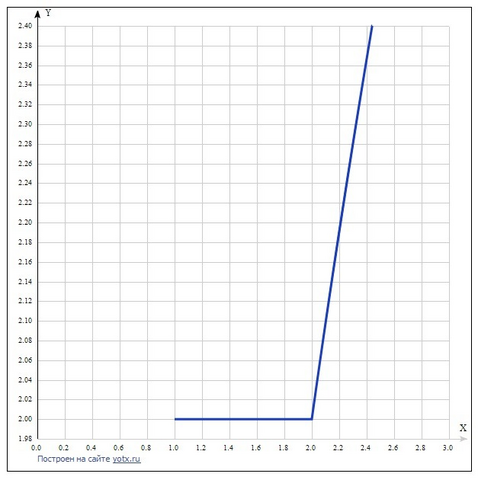
Дано выражение √(x - 2√(x - 1)) + √(x + 2√(x - 1)).
Значение его примем за у.
у = √(x - 2√(x - 1)) + √(x + 2√(x - 1)).
Возведём обе части в квадрат.
у² = x - 2√(x - 1)) + x + 2√(x - 1)) + 2*√(x - 2√(x - 1)) *√(x + 2√(x - 1)).
При х больше 1 можно сократить на 2√(x - 1)).
у² = 2x + 2*√(x² - 4(x - 1)) = 2x + 2*√(x² - 4x + 4).
Подкоренное выражение - полный квадрат:
у² = 2x + 2*√((x - 2)²).
Теперь для определения значения у надо извлечь корень.
При решении иррациональных уравнений учитываем формулу:
√(a²) = |a|.
у = √( 2x + 2*√((x - 2)²)) = √(2х + 2*|x - 2|)
Получаем 2 варианта: y =√(2х + 2x - 4) = √(4х - 4) = 2√(х - 1)
и у = √(2х - 2x + 4) = 2.
Первый вариант из условия корня в выражении √((x - 2)²) применим при условии x ≥ 2.
Но по заданию х = 1,2007, поэтому применяем второй вариант и получаем ответ:
значение заданного выражения при х = 1,2007 равно 2.