Преобразуем числитель: 
 0" alt="\frac{(x-4)(x+4)}{(x-6)^2}>0" align="absmiddle" class="latex-formula">
0" alt="\frac{(x-4)(x+4)}{(x-6)^2}>0" align="absmiddle" class="latex-formula">
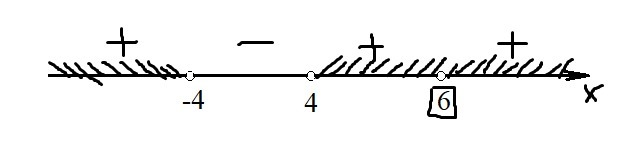
Решим методом интервалов. Отметим на числовой прямой нули неравенства (см. рис.)
Так как x = 6 - корень чётной степени, проходя через него, знак выражения не меняется.
Решением будет промежуток 
Пересекая с промежутком ![x\in[-6; 6] x\in[-6; 6]](https://tex.z-dn.net/?f=x%5Cin%5B-6%3B%206%5D) , получим
, получим  . Целые числа, принадлежащие данному промежутку: -6, -5, 5, т. е. 3 числа.
. Целые числа, принадлежащие данному промежутку: -6, -5, 5, т. е. 3 числа.
Ответ: 4)