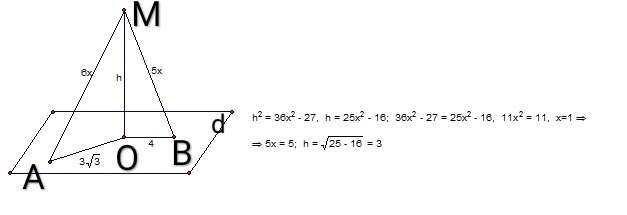Пусть даны наклонные MА и MB и перпендикуляр к плоскости MО. Если х - коэффициент пропорциональности, то MВ=5х, MА=6х. Проецией наклонной MВ является отрезок ВО=4 см, а проекцией наклонной MА является отрезок AО=3√3. Найдем АО из треугольника АMО по теореме Пифагора: MО² = MA² - AO² = 25x² - 16; найдем MО из треугольника BMО по теореме ПИфагора: MО² = MB² -BO² = 36x² - 27. Приравняем правые части получившихся выражений 25х² - 16=36x² - 27
11x² = 11
x = 1 - коэффициент пропорциональности, то MA = 5 см; MB = 6 см и MO = 3 см
Ответ: 3 см