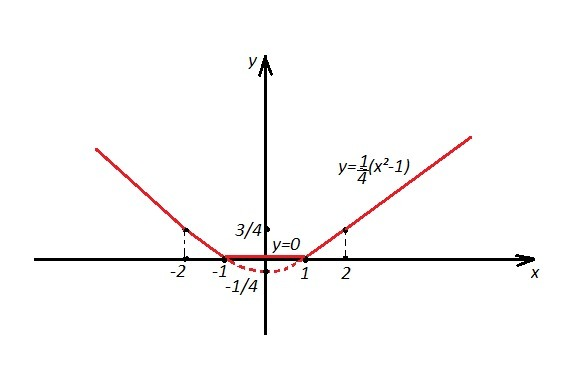
Выражение под модулем x²-1≥0 , (х-1)(х+1)≥0, при х∈ (-∞, -1)∪(1,+∞) . Тогда |x²-1|=x²-1 и функция примет вид
 .
.
Значит левее точки х= -1 и правее точки х=1 надо начертить график параболы  .
.
Если х²-1<0, (x-1)(x+1)<0 , при <img src="https://tex.z-dn.net/?f=x%5Cin%20%28-1%2C1%29" id="TexFormula4" title="x\in (-1,1)" alt="x\in (-1,1)" align="absmiddle" class="latex-formula"> , то  и функция примет вид
и функция примет вид  . Значит, на интервале х∈( -1,1) надо нарисовать прямую у=0 ( это уравнение оси ОХ).
. Значит, на интервале х∈( -1,1) надо нарисовать прямую у=0 ( это уравнение оси ОХ).
На рисунке график обведён сплошной красной линией. (Штриховая красная линия - это линия, оставшаяся от параболы, на интервале (-1,1) она заменена прямой у=0.)