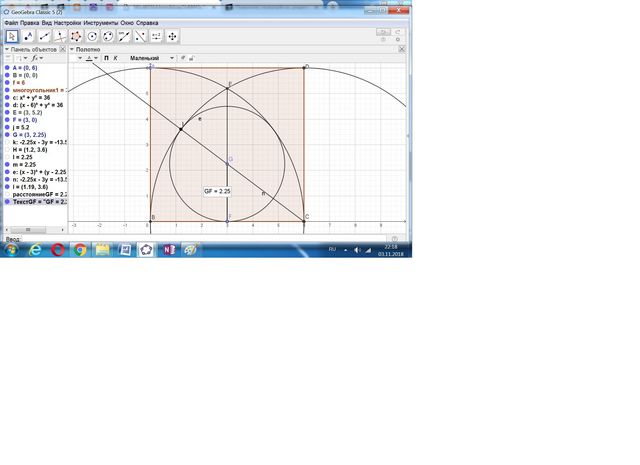
Пусть имеем квадрат АВСД со стороной а и 2 окружности радиусом а с центрами в точках А и Д.
Обозначим радиус заданной окружности за r, центр - точка О.
Из точки О проводим радиус ОЕ, перпендикулярный АД и радиус большой окружности ДОР.
Так как РО = r, то ОД = а - r.
В треугольнике ОЕД радиус ОЕ = r, точка Е находится еа середине АД, поэтому ЕД = а/2.
По Пифагору ОЕ² + ЕД² = ОД².
Заменим их значениями.
r² + (а/2)² = (а - r)².
r² + (а²/4) = а² - 2аr + r².
Получаем 8аr = 3а².
Ответ: r = (3/8)а.