Ответ:
∠АВС = 45°.
Объяснение:
В задачах, где в условии даны только отношения, угол обычно определяется также через отношения, то есть через тригонометрическую функцию.
Попробуем "приблизить" угол В к треугольнику AЕD с его медианами.
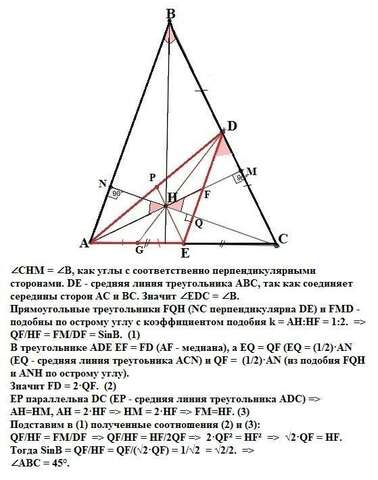
Заметим, что ∠СНМ = ∠В, как углы с соответственно перпендикулярными сторонами. DE - средняя линия треугольника АВС, так как соединяет середины сторон АС и ВС. Значит ∠EDC = ∠B.
Прямоугольные треугольники FQH (NC перпендикулярна DE) и FMD - подобны по острому углу c коэффициентом подобия k = AH:HF = 1:2. =>
QF/HF = FM/DF = SinB. (1)
В треугольнике ADE EF = FD (AF - медиана), а EQ = QF (EQ = (1/2)·AN (EQ - средняя линия треугоьника ACN) и QF = (1/2)·AN (из подобия FQH и ANH по острому углу).
Значит FD = 2·QF. (2)
ЕР параллельна DC (ЕР - средняя линия треугольника ADC) =>
AH=HM, AH = 2·HF => HM = 2·HF => FM=HF. (3)
Подставим в (1) полученные соотношения (2) и (3):
QF/HF = FM/DF => QF/HF = HF/2QF => 2·QF² = HF² => √2·QF = HF.
Тогда SinB = QF/HF = QF/(√2·QF) = 1/√2 = √2/2. =>
∠B = 45°.
Вариант 2. По теореме Менелая.
В треугольнике AFE и секущей HC:
(AH/HF)·(FQ/QE)·(EC/CA) =1 или (2/1)·(FQ/QE)·(1/2) =1. => FQ=QE.
Тогда, так как EF=FD (AF -медиана), то FD = 2·FQ.
В треугольнике EDC и секущей AM:
(CM/MD)·(DF/FE)·(EA/AC) =1 или (CM/MD)·(1/1)·(1/2) =1. => CM/MD = 2/1.
В треугольнике САМ и секущей ED:
(CE/EA)·(AF/FM)·(MD/DC) =1 или (1/2)·(AF/FM)·(1/3) =1. => AF/FM =3/1.
Тогда, так как АН/HF = 2/1 (AF -медиана), то HF = FM.
Подставим в (1) полученные соотношения:
QF/HF = HF/(2·QF) => 2QF² = HF² => HF = QF√2.
SinB = QF/HF = QF/(QF√2) = 1/√2 = √2/2. =>
∠B = 45°.