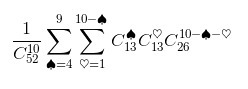Из колоды 52 карты достали 10 карт, какая вероятность что хотя бы 4 карты пиковые и хотя...

Question

Из колоды 52 карты достали 10 карт, какая вероятность что хотя бы 4 карты пиковые и хотя бы одна червовая. Я бы вообще все балы отдал, очень нужно решение.

Comments

А можно побольше объяснений, ведь всего в колоде 36 карт

---

23456789TJQKA = 13*4 = 52. Даже понятно что копать надо в сторону гипергеометрического распределения, но типовых задач прямо вообще не нагуглить

---

ну какая разница, господи учитель скажет карт не 36, а 52, поменяете цифру, ему ж расчеты-формул важны, а не 0.234234 или как оно там -)

Answer 1

в колоде 4 масти по 13 карт каждая.

Можно посчитать впрямую карты:

4 пика и 1 черви

4 пика и 2 черви

***********

5 пика и 1 черви

5 пика и 2 черви

и т.д.

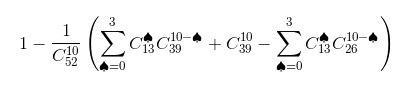
А можно считать от обратного(от обратного меньше циклов подсчета):

0 черви и все угодно

1 черви 3 пики

1 черви 2 пики

*****

2 черви 3 пики

и т.д.

Потом довычислить "искомый шанс"=1-"обратный шанс"

Решил вместе с nelle987

Два рисунка формулы, там начинается с "1-" это естественное расчет от обратного.

---

---

Comments

Ааа 1-((m0+m1+m2)/ц) это уже ответ? если так то там получается ~98 мб я просто логики не уловил. (Хотя если просто воткнуть в эту формулу m=4 n =10 M=13 N=52 то ответ получится 0.2042716. И так как условия зависимые он уменьшится, но незначительно но как и куда воткнуть второе условие задачи вообще не понятно.)

---

я не уверен, но уже ночь думать не могу про масти. Кажется решил с условиями, что "4 карты пиковые и хотя бы одна червовая" или "4 карты бубновые и хотя бы другой масте", тоесть не под конкретную масть, и тут надо шанс еще в несколько раз(в четыре раза?). Это уже сам подумай, завтра спишемся на свежую голову.