Уравнение высоты:  , значит, уравнение противолежащей стороны будет выглядеть так:
, значит, уравнение противолежащей стороны будет выглядеть так:  . Зная, что сторона проходит через точку (4; 6), найдём b:
. Зная, что сторона проходит через точку (4; 6), найдём b:  . То есть
. То есть  - уравнение одной из сторон.
- уравнение одной из сторон.
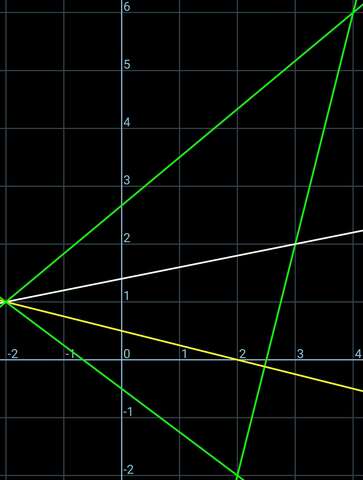
Медиана пересекает сторону в точке (3; 2). Вычислим координаты второй вершины:  .
.
Найдём третью вершину - точку пересечения медианы и высоты. Они пересекаются в точке (-2; 1).
Найдём уравнения остальных сторон по уравнению прямой  :
:
1) Сторона, соединяющая точки (4; 6) и (-2; 1): 
2) Сторона, соединяющая точки (2; -2) и (-2; 1): 
Найдём точку пересечения высоты и противолежащей стороны (выразим их через y и приравняем):

Длина высоты 
Ответ: вершины: (4; 6), (2; -2), (-2; 1); уравнения сторон:  ,
,  ,
,  ; длина высоты:
; длина высоты: