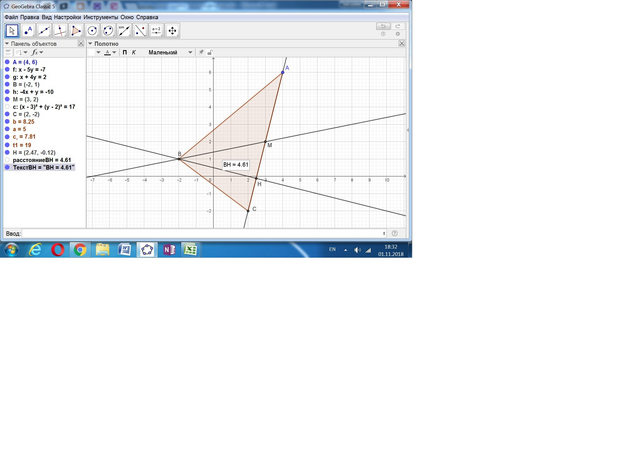
Дано: вершина А(4,6), уравнения медианы x-5y+7=0 и высоты x+4y-2=0 выходящих из одной вершины.
Находим координаты вершины В, из которой выходят медиана и высота, приравняв их уравнения.
x-5y+7= x+4y-2,
9у = 9,
у = 9/9 = 1, х = 2 - 4у = 2 - 4*1 = -2.
Точка В(-2; 2).
Сторона АС перпендикулярна заданной высоте ВН = x+4y-2=0.
Уравнение высоты ВН выразим относительно у: у = (-1/4)х + (1/2).
Угловой коэффициент стороны АС равен:
к(АС) = -1/к(ВН) = -1/(*1/4) = 4.
Тогда уравнение АС имеет вид у = 4х + в.
Для определения величины"в" подставим координаты точки А, которые нам известны.
6 = 4*4 + в, отсюда в = 6 - 16 = -10.
АС: у = 4х - 10.
Найдём координаты точки М - основание заданной медианы.
Уравнение медианы ВМ x-5y+7 = 0 выразим так: у = (1/5)х + (7/5).
Приравняем уравнения АС и ВМ: 4х - 10 = (1/5)х + (7/5).
20х -50 = х + 7,
19х = 57, х = 57/19 = 3, у = 4*3 - 10 = 2.
Точка М(3; 2).
Находим координаты точки С как симметричной точке А относительно точки М: хС = 2хМ - хА = 2*3 - 4 = 2,
уС = 2уМ - уА = 2*2 - 6 = -2.
Точка С(2; -2).
Расчет длин сторон:
АВ (с) =√((Хв-Ха)²+(Ув-Уа)²) =√61 = 7,810249676,
BC (а)=√((Хc-Хв)²+(Ус-Ув)²) =√25 = 25
,
AC (в) =√((Хc-Хa)²+(Ус-Уa)²) =√68 = 8,246211251.
По формуле Герона определяем площадь треугольника АВС.
S = √(p(p-a)(p-b)(p-c)). Подставив данные, получаем S = p = 10,52823,
S = 19.
Отсюда находим длину высоты ВН:
ВН = 2S/AC = 2*19*/√68 = 38/√68.
Уравнения сторон:
АВ: (х - 4)/6 = (у - 6)/5,
ВС: (х + 2)/4 = (у - 1)/(-3),
АС: (х - 4)/2 = (у -6)/8, или, сократив на 2 имеем (х - 4)/1 = (у -6)/4.