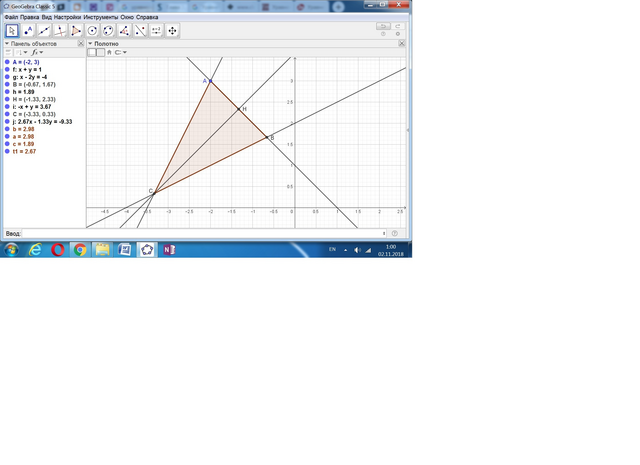
Дано: уравнение основания равнобедренного треугольника х+у-1=0, боковой его стороны х-2у+4=0, точка А(-2;3) лежит на второй его стороне. Найти её уравнение.
Находим координаты точки В на основании треугольника, приравнивая уравнения основания и боковой стороны.
х + у - 1 = х - 2у + 4,
3у = 5, у = 5/3.
х = 1 - у = 1 -(5/3) = -2/3.
Точка В((-2/3); (5/3)).
Находим координаты точки Н как середины отрезка АВ.
Н((-2+(-2/3))/2 = -8/6 = -4/3; (3+(5/3)/2 = 14/6 = 7/3) = ((-4/3); (7/3)).
Угловой коэффициент прямой СН как высоты равнобедренного треугольника равен: к(СН) = -1/к(АВ).
Выразим уравнение АВ относительно у: у = -х + 1. к(АВ) = -1.
Тогда к(СН) = -1/-1 = 1.
Уравнение СН имеет вид у = х + в.
Для определения величины "в" подставим координаты точки Н:
7/3 = 1*(-4/3) + в, в = (7/3) + (4/3) = 11/3.
Получаем уравнение СН: у = х + (11/3) или в общем виде 3х - 3у + 11 = 0.
Теперь можно получить координаты точки С как точку пересечения прямых ВС и СН, выраженных относительно у.
ВС: у =(1/2)х + 2, СН: у = х + (11/3).
(1/2)х + 2 = х + (11/3),
х - (1/2)х = 2 - (11/3),
(1/2)х = -5/3,
х = (-5/3)/(1/2) = -10/3, у = х + (11/3) = (-10/3) + (11/3) = 1/3.
Точка С((1/3); (-5/3)).
По координатам двух точек А и С определяем уравнение этой прямой.
АС: (х + 2)/((-10/3)+2) = у - 3)/((1/3)-3)
АС: (х + 2)/(-4/3) = (у - 3)/(-8/3), после сокращения на (-4/3) получаем каноническое уравнение:
АС: (х + 2)/1 = (у - 3)/2.
В общем виде 2х + 4 = у - 3 или 2х - у + 7 =0.