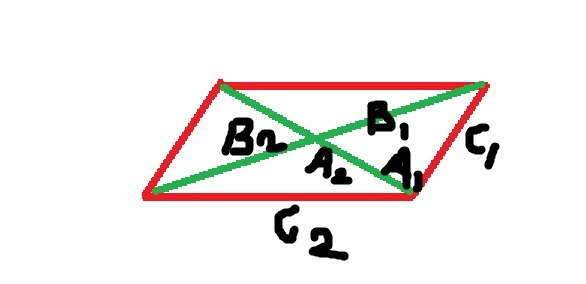
В получившихся треугольниках одна сторона будет общая и равная А1=А2, еще одна сторона у каждого треугольника будет образована частями диагонали, разделенной точкой пересечения пополам, значит и эти стороны будут равны В1=В2. Периметры треугольников будут равны А1+В1+С1 и А2+В2+С2, а их разница будет равна (А1+В1+С1) - (А2+В2+С2) и по условию задания будет равно 2.
Заменим стороны равные друг другу А1=А2 и В1=В2:
(А1+В1+С1)-(А1+В1+С2)=2
А1+В1+С1-А1-В1-С2=2
С1-С2=2
С1=2+С2
Стороны треугольников С1 и С2 являются сторонами параллелограмма, Периметр параллелограмма равен
2*С1+2*С2 = 28
2*(2+С2)+2*С2=28
4+2*С+2*С2=28
4*С2=28-4
4*С2=24
С2=6
С1 = 6+2=8
Стороны параллелограмма равны 6 и 8 см.