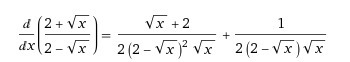Сначала функция g(x) - полином.
ПРАВИЛО: Производная суммы равна сумме производных.
Записываем функцию g(x) в виде полинома - в степенях.
g(x) = 1/5*x³/⁴ - 2*x⁻¹/³ + x⁶/⁵
Теперь дифференцируем степени - важно не ошибиться.
g'(x) = (1/5*3/4)*x⁻¹/⁴ - (2*-1/3)*x⁻⁴/³ + (6/5)*x¹/⁵
Пробуем записать в виде радикалов.
![g'(x)= \frac{3}{20\sqrt[4]{x}} + \frac{2}{3x\sqrt[3]{x}}+ \frac{6\sqrt[5]{x}} {5}](https://tex.z-dn.net/?f=g%27%28x%29%3D%20%5Cfrac%7B3%7D%7B20%5Csqrt%5B4%5D%7Bx%7D%7D%20%2B%20%5Cfrac%7B2%7D%7B3x%5Csqrt%5B3%5D%7Bx%7D%7D%2B%20%5Cfrac%7B6%5Csqrt%5B5%5D%7Bx%7D%7D%20%7B5%7D "g'(x)= \frac{3}{20\sqrt[4]{x}} + \frac{2}{3x\sqrt[3]{x}}+ \frac{6\sqrt[5]{x}} {5}")
Функцию f(x) можно записать как произведение двух функций. (Можно как и частное).
f(x) =u(x)*v(x) = (2+√x) * (2-√x)⁻¹
Правило дифференцирования: f'(x) = u'(x)*v(x) + v'(x)(*u(x).
Запись уравнения на рисунке в приложении.
