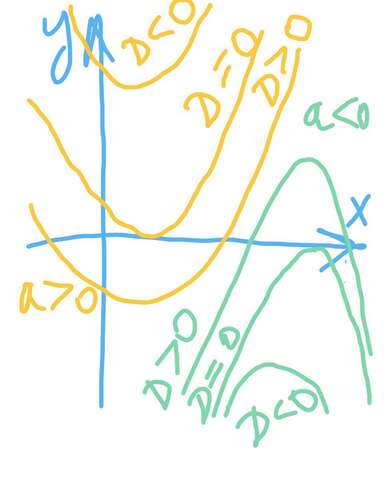
как мы видим из графиков при разных значениях коэффициента а и дискриминанта D квадратного уравнения


график будет над осью абсцисс при:

0} \atop {D = (a - 3) ^{2} - 4 {a}^{2} < 0}} \right. \\ \left \{ {{a > 0} \atop { (a - 3- 2 {a} )(a - 3 + 2a) < 0}} \right. \\ \left \{ {{a > 0} \atop { ( - 3- {a} )(3a - 3 ) < 0}} \right. \\ \left \{ {{a > 0} \atop { ( {a} + 3 )(a - 1 ) > 0}} \right. \\ " alt="\left \{ {{a > 0} \atop {D = (a - 3) ^{2} - 4 {a}^{2} < 0}} \right. \\ \left \{ {{a > 0} \atop { (a - 3- 2 {a} )(a - 3 + 2a) < 0}} \right. \\ \left \{ {{a > 0} \atop { ( - 3- {a} )(3a - 3 ) < 0}} \right. \\ \left \{ {{a > 0} \atop { ( {a} + 3 )(a - 1 ) > 0}} \right. \\ " align="absmiddle" class="latex-formula">
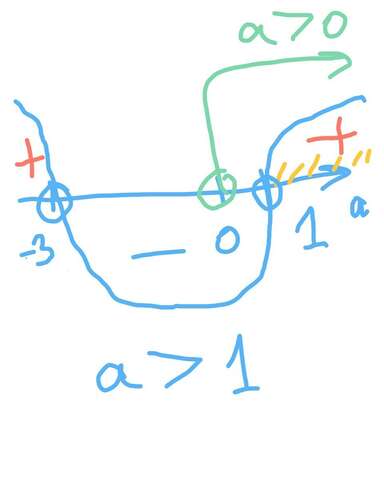
решаем методом интервалом (см рисунок)
Ответ:
при а>1