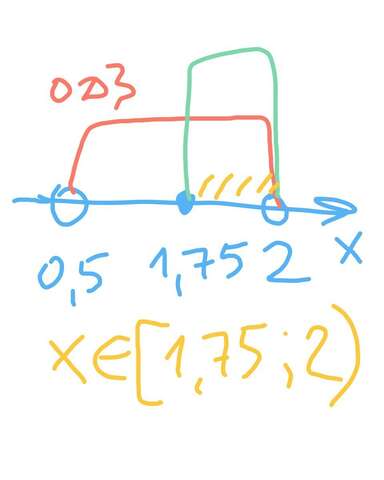Помогите срочно..........

$lg(lg( \frac{2x - 1}{2 - x} )) \geqslant 0 \\ lg( \frac{2x - 1}{2 - x} ) \geqslant 1 \\ \frac{2x - 1}{2 - x} \geqslant 10 \\ \frac{2x - 1 - 20 + 10x}{2 - x} \geqslant 0 \\ \frac{12x - 21}{x - 2} \leqslant 0 \\ \frac{12(x - \frac{7}{4} )}{x - 2} \leqslant 0 \\ \frac{x - 1.75}{x - 2} \leqslant 0$
решаем методом интервалом

решением (без учёта ОДЗ!)
будет
2>х≥1,75 ( Зелёная область, см рисунок)

теперь найдем ОДЗ:

0 \\ \frac{2(x - 0.5)}{x - 2} < 0" alt=" \frac{2x - 1}{2 - x} > 0 \\ \frac{2(x - 0.5)}{x - 2} < 0" align="absmiddle" class="latex-formula">
ОДЗ:
решаем это неравенство
тоже методом интервалов
2>х>0,5 ( см рисунок, красная область)

Окончательным решением будет пересечение этих интервалов:

x \geqslant 1.75} \atop {2 > x > 0.5}} \right. " alt="\left \{ {{2 > x \geqslant 1.75} \atop {2 > x > 0.5}} \right. " align="absmiddle" class="latex-formula">
или

2>x≥1,75

Ответ x∈[1,75; 2)