Помогите решить. Даю 50 балов.

$\frac{x^2-6x+8}{x-1}-\frac{x-4}{x^2-3x+2}\leq0$

ОДЗ: х-1 ≠0 => x ≠ 1

x²-3x+2 ≠ 0 => x ≠ 1; x≠ 2

Общее: х ≠ 1: x≠ 2

$\frac{x^2-6x+8}{x-1}-\frac{x-4}{x^2-3x+2}\leq0\\\\\frac{x^2-6x+8}{x-1}-\frac{x-4}{(x-1)(x-2)}\leq0\\\\\frac{(x^2-6x+8)(x-2)-(x-4)}{(x-1)(x-2)}\leq0\\\\\frac{(x-2)(x-4)(x-2)-(x-4)}{(x-1)(x-2)}\leq0\\\\\frac{(x-4)((x-2)^2-1)}{(x-1)(x-2)}\leq0\\\\\frac{(x-4)(x-2-1)(x-2+1)}{(x-1)(x-2)}\leq0\\\\\frac{(x-4)(x-3)(x-1)}{(x-1)(x-2)}\leq0;(x\neq1)\\\\\frac{(x-4)(x-3)}{x-2}\leq0$

Далее решаем методом интервалов.

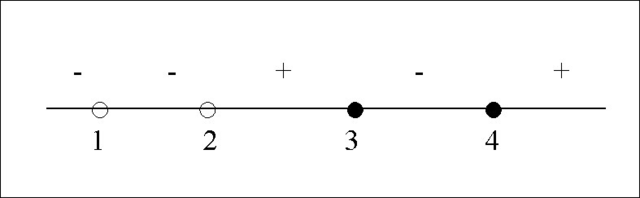
На числовой прямой отмечаем точки:

х≠1; х≠ 2; х=3; х=4

Получили 5 промежутков, определяем знак на каждом из них:

1) (-∞; 1)

при х = 0 получаем (- × - )/ - = "-" минус

2) (1; 2)

при х = 1,5 получаем (- × - )/ - = "-" минус

3) (2; 3]

при х = 2,5 получаем (- × - )/ + = "+" плюс

4) [3; 4]

при х = 3,5 получаем (- × + )/ + = "-" минус

5) [4; +∞)

при х = 5 получаем (+ × + )/+ = "-" плюс

Ответ: x ∈ (-∞; 1)∪(1; 2)∪[3; 4]