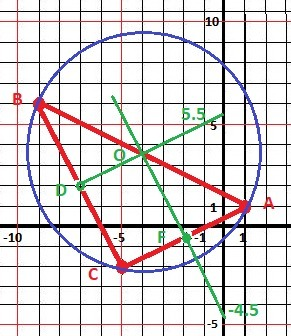
ДУМАЕМ - центр описанной окружности на пересечении высот из середин сторон треугольника.
Рисунок к задаче в приложении.
1) Координаты точки F - середина АС - F = (C+A)/2)
Fx = (- 5 +1)/2 = -2 и Fy= (-2+1)/2 = - 0.5 и F(-2;-0.5)
2) Ищем уравнение перпендикуляра FO.
a) Наклон прямой АС = k1 = (Ay-Cy)/(Ax-Cx) = 3/6 = 1/2.
Наклон перпендикуляра - k2 = - 1/k1 = - 2.
Сдвиг прямой FO по оси У. b = Fy - k2*Fx) = - 0.5 - (-2)*(-2) = - 4.5
Уравнение FO: Y = -2*x - 4.5 - первая линия.
б) Аналогично для прямой DO.
D= (B+C)/2, D(-7;2) - середина стороны ВС.
k(BC) = 8/(-4) = - 2, k(DO) = 1/2 - наклон DO.
b(DO) = Dy - k(BC)*Dx) = 2 - 1/2*(-7) = 5.5
Уравнение прямой DO: Y = 0,5*x + 5.5.
в) Находим точку пересечения прямых FO и DO.
Применим метод подстановки - приравняем уравнения прямых и получим:
-2*х - 4,5 = 0,5*х + 5,5 и 2,5*х = - 10 и х = - 4 - и подставим в любое уравнение прямой.
у =- 2*(-4) - 4,5 = 3,5
Получили координаты центра окружности - О(-4;-3,5)
г) Вычисляем радиус окружности по теореме Пифагора - расстояние до любой из вершин, например, до вершины А.
(ОА)² = (Oy-Ay)² + (Ox-Ax)² = (2.5)² + 5² = 31.25
R = √31.25 ≈ 5.6 - радиус описанной окружности - ОТВЕТ
ДУМАЕМ - центр вписанной окружности - точка пересечения биссектрис треугольника. Радиус окружности по формуле:
r = S/p, где : S- площадь, p = (a+b+c)/2 - полупериметр.
Находим длины сторон по формуле Пифагора.
Находим площадь по формуле: S = a*h - нужно найти одну из высот треугольника.