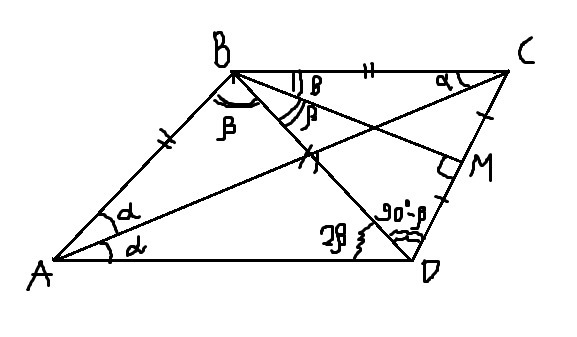
Пусть ∠A = 2α, ∠B = 3β. ∠BAC = ∠CAD, так как AC - биссектриса. ∠CAD = ∠BCA как накрест лежащие. Отсюда ∠BAC = ∠BCA ⇒ AB = BC.
В треугольнике BCD BM - медиана и биссектриса ⇒ BC = BD, BM - высота.
AB = BC, BC = BD ⇒ AB = BD ⇒ ∠A = ∠ADB. ∠A = 2α, ∠ADB = ∠CBD = ∠CBM + ∠DBM = β + β = 2β ⇒ 2α = 2β ⇔ α = β.
В треугольнике ABD по теореме о сумме углов треугольника ∠A + ∠ADB + ∠ABD = 180° ⇒ 2α + 2β + β = 2α + 3β = 180°. Т. к. α = β, то 2α + 3α = 5α = 180° ⇒ α = β = 36° ⇒ ∠A = 72°, ∠B = 108°.
В прямоугольном треугольнике BMD ∠BDM = 90° - ∠DBM = 90° - β.
∠D = ∠BDA + ∠BDM = 2β + 90° - β = β + 90° = 126°
∠C + ∠D = 180° как внутренние односторонние ⇒ ∠C = 180° - ∠D = 180° - 126° = 54°.
Ответ: ∠A = 72°, ∠B = 108°, ∠C = 54°, ∠D = 126°