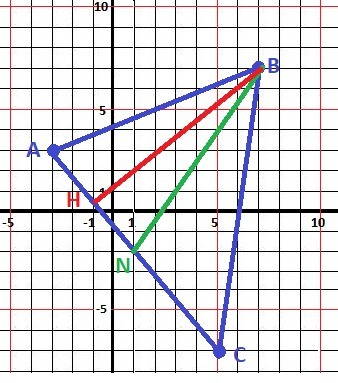
Рисунок к задаче в приложении.
ДУМАЕМ
1. нужны уравнения прямых BN - медианы и BH - высоты.
2. Медиана BN - нужны координаты точки N - середина АС.
3. Высота ВН - перпендикулярна прямой АС. Нужно уравнение прямой АС.
РЕШЕНИЕ
1) Nx = (Ax+Cx)/2 = 1 и 2) Ny = (Ay+Cy)/2 = -2 и точка N(1;-2).
2) k(BN) = (By-Cy)/(Bx-Cx) = 3/2 = 1.5 - наклон медианы
3) k(AC) = - 5/4 = - 1 1/4 - наклон стороны АС.
4) k(BH) = - 1/k(AC) = 4/5 - наклон высоты ВН
5) Угол по формуле tgα = (k2 - k1)/(1 + k1*k2)
k2 - k1 = 7/10,
1+k1*k2 = 2 1/5
tgα = 7/22
arctg(7/22) = 0.308 рад = 17,65 град - ОТВЕТ