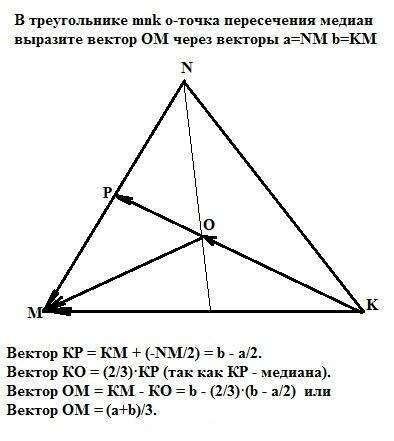
Ответ:
Вектор ОМ = (a+b)/3.
Объяснение:
Вектор КР = КМ + МР.
Вектор МР = (1/2)·( -NM) так как ьочка Р - середина стороны MN, а вектор MN направлен противоположно вектору NM. Тогда
КР = КМ -NM/2 = b - a/2. (по правилу сложения векторов).
Вектор КО = (2/3)·КР = (2/3)·(b - a/2) (так как КР - медиана и делится точкой Р в отношении 2:1, считая от вершины).
Вектор ОМ = КМ - КО = b - (2/3)·(b - a/2) или
Вектор ОМ = (a+b)/3.