Рассмотрим данные нам числа.
→ Внесём 5 в первом числе и 7 во втором под корень.
1. 
2. 
→ Рассмотрим ближайшие к полученным корням числа, составим неравенства.
1.  , значит
, значит  лежит между числами 13 и 14.
лежит между числами 13 и 14.
2.  , значит
, значит  лежит между числами 15 и 16.
лежит между числами 15 и 16.
→ Таким образом, имеем следующее.
1.  лежит между числами 13 и 14.
лежит между числами 13 и 14.
2.  лежит между числами 15 и 16.
лежит между числами 15 и 16.
Пусть  ≈ 13,5 и
≈ 13,5 и  ≈ 15,5. Мы рассматриваем только целые числа, поэтому нам не особо важна дробная часть этих чисел.
≈ 15,5. Мы рассматриваем только целые числа, поэтому нам не особо важна дробная часть этих чисел.
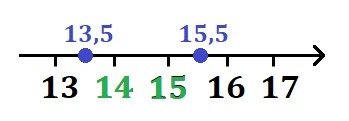
→ Так какие же числа лежат между 13,5 и 15,5?
Проще всего понять это взглянув на числовую прямую. Её я добавил в приложения. Между данными числами лежат ровно два целых числа.
Значит, подходящие нам числа: 14 и 15.
Ответ: 2 целых числа, а именно 14 и 15.