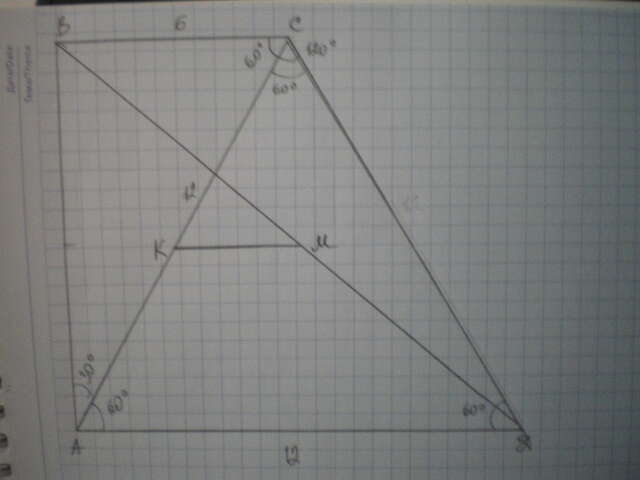
Дано: АВСД - трапеция, ∠А=∠В=90°; ∠С=120°; АД=АС=12 см.
Найти КМ.
Решение: Отрезок, соединяющий середины диагоналей трапеции, численно равен половине их разности. Задача сводится к нахождению основания ВС.
Рассмотрим ΔАСД - равнобедренный, с основанием СД.
∠СДА=180-120=60°, т.к. сумма углов, прилежащих к одной стороне трапеции, равна 180°.
Поскольку углы при основании равнобедренного треугольника равны, то ∠АСД=∠СДА=60°.
Рассмотрим ΔАВС - прямоугольный, ∠АСВ=120-60=60°, тогда ∠САВ=90-60=30°.
Катет ВС лежит против угла 30°, поэтому равен 1\2 АС=6 см.
КМ=(12-6):2=3 см.
Ответ: 3 см.