Решите пожалуйста. Тело,двигаясь по окружности радиусом 20м,прошло четверть круга....

Дано:

Радиус окружности: R = 20 м.

Пройденный путь: S = L/4.

Найти путь S - ? и модуль перемещения r - ?

А также определить отношение скоростей: / - ?

Решение:

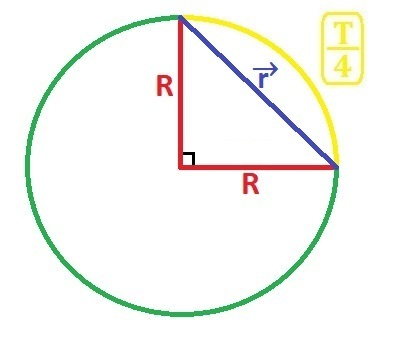
0. Немного фирменных рисунков, смотри приложение.

1. Чтобы найти путь для начала найдём длину окружности. Формула длины окружности: L = 2πR.

2. Путь, пройденный телом - четверть длины окружности: $S = \frac{L}{4} = \frac{2\pi R}{4} = \frac{\pi R}{2}.$

3. Перемещение найдём по теореме Пифагора (см. приложение): $r = \sqrt{R^2 + R^2} = \sqrt{2R^2} = R\sqrt{2}.$

4. Средняя путевая скорость: = \frac{S}{t}." alt=" = \frac{S}{t}." align="absmiddle" class="latex-formula">

5. Средняя скорость по перемещению: = \frac{r}{t}." alt=" = \frac{r}{t}." align="absmiddle" class="latex-formula">

6. Искомое отношение: }{} = \frac{S*t}{t*r} = \frac{S}{r} = \frac{\pi R}{2R\sqrt2} = \frac{\pi}{2\sqrt2}." alt="\frac{}{} = \frac{S*t}{t*r} = \frac{S}{r} = \frac{\pi R}{2R\sqrt2} = \frac{\pi}{2\sqrt2}." align="absmiddle" class="latex-formula">

Численно получаем:

$S = \frac{3,14*20}{2} = 3,14 * 10 = 31,4$ (м).

$r = 20*\sqrt{2} = 28,3$ (м).

}{} = \frac{\pi}{2\sqrt2} = \frac{3,14}{2*1,41} = 1,11." alt="\frac{}{} = \frac{\pi}{2\sqrt2} = \frac{3,14}{2*1,41} = 1,11." align="absmiddle" class="latex-formula">

Решите пожалуйста. Тело,двигаясь по окружности радиусом 20м,прошло четверть круга....

Дано:

Решение:

Численно получаем:

Ответ: 31,4 м; 28,3 м; 1,11.