Задача 1.
Радиус вписанной окружности по формуле

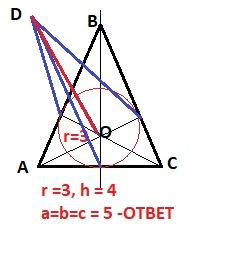
Рисунок к задаче в приложении.
Получаем треугольники со сторонами 3:4:5 - "египетский"
ОТВЕТ 5 см одинаково для всех сторон.
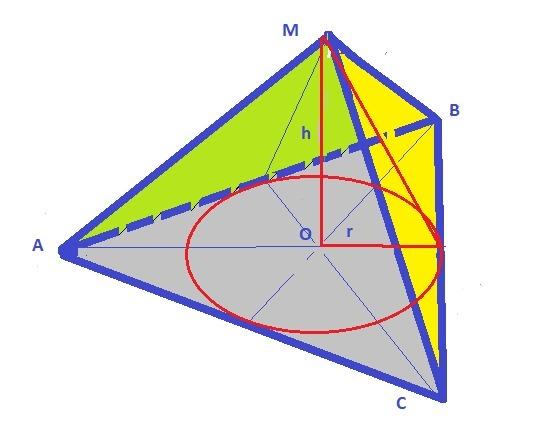
2. Рисунок к задаче в приложении. (Вариант годится и для первой задачи.)
1) Радиус вписанной окружности для правильного треугольника по формуле:
 2) Расстояние до сторон по теореме Пифагора:
2) Расстояние до сторон по теореме Пифагора:
L² = (√3/2)² + (√3)² = 3 3/4 = 15/4
L = √(15/4) = 1/2*√3*√5 - расстояние до сторон - ОТВЕТ