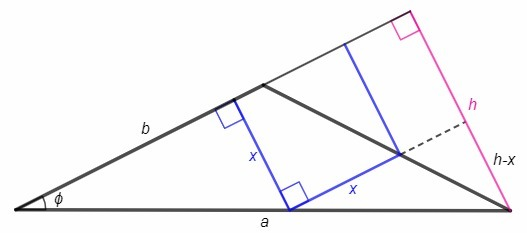
Равнобедренный треугольник, основание a=289, боковая сторона - b, угол при основании - ф, sinф=5/13.
Высота к боковой стороне - h.
Сторона квадрата, параллельная боковой стороне треугольника, отсекает подобный треугольник, его высота к боковой стороне равна h-x.
x/b=(h-x)/h <=> x/b +x/h =1 <=> x=bh/(b+h)
sinф=5/13 <=> cosф=12/13 (пифагорова тройка 5, 12, 13)
cosф=(a/2)/b <=> b=a/2cosф =a*13/24
h=a*sinф =a*5/13
x= a*5/24 : (13/24 +5/13) =a*65/289 =65