task/30078961 Построить график функции y = (x² - x+2) / | x+1 | .
решение y=(x²-x+2) / |x+1| D(y) : x +1 ≠ 0 , т.е. x∈ (-∞ ; -1) ∪ ( -1 ; + ∞)
на D(y) y=(x²-x+2) / |x+1| =( (x-0,5)² +1,75 ) / |x+1| > 0 .
y= (x²-x+2) / |x+1|= ( (x-2)(x+1) +4 ) / |x+1| = ( x-2) (x+1) / |x+1+ 4 / |x+1|
y = - x + 2 - 4 / (x+1) , если x < -1 . x → -1 -0 ; y ⇒ +∞ и x → -∞ ; y ⇒ +∞
y ' = -1 +4/(x+1)² = (x+3)(1 -x) / (x+1)² ; min y =y(-3) = 7
y = x - 2 + 4/ (x +1) , если x > -1 . x → -1 +0 ; y ⇒ +∞ и x → ∞ ; y ⇒ ∞
y' = 1 -4/(x+1)² = (x+3) (x-1) / (x+1)² ; min y = y(1) = 1.
вертикальный асимптот x = - 1 ;
наклонные асимптоты y = - x +2 и y = x -2 .
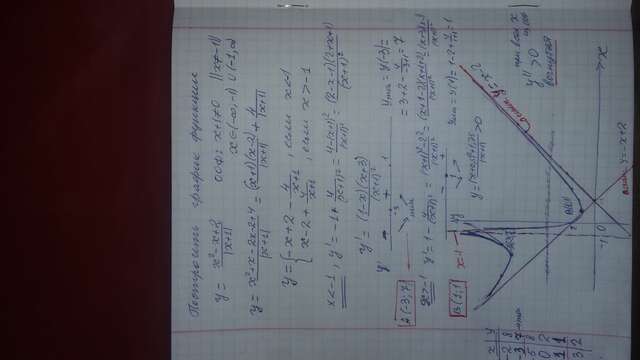
схематический график см ПРИЛОЖЕНИЕ
(-2; 8) , (-3; 7) , (-5; 8) , (0 ,2) , B(1 ; 1) ; (3;2) ∈ Г