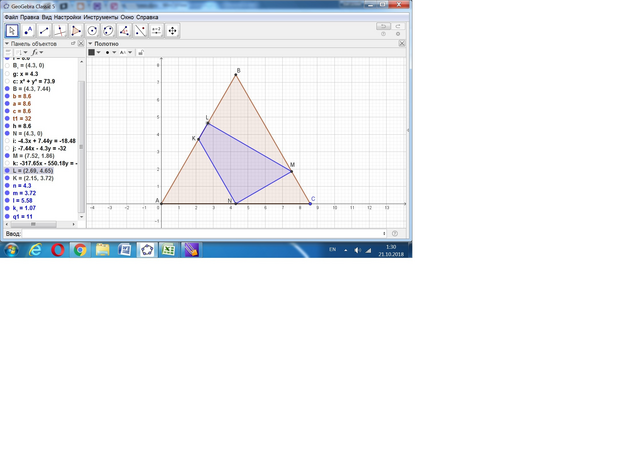
Для удобства расчётов примем 1/8 часть стороны треугольника за х.
Площадь четырехугольника KLMN легче определить вычитанием трёх треугольников из заданного.
Стороны треугольника АKN равны половине исходного, тогда S1 = (1/4) *32 = 8 см².
Используя свойства прямоугольных треугольников с углами 60 и 30 градусов, находим площади треугольников BLM и CNM.
S(BLM) = (1/2)*3x*3√3x = (9/2)√3x² см²,
S(CNM) = (1/2)*2x*2√3x = 2√3x² см².
Их сумма равна S2 + S3 = (9/2)√3x² + 2√3x² = (13/2)√3x² см².
Сторону исходного треугольника определяем на основе формулы площади равностороннего треугольника.
S = a²√3/4.
a = √(4S/√3) = √(4*32/√3) = 8√(2/√3).
Так как х = а/8, то х² = а²/64 = 64(2/√3)/64 = (2/√3).
Находим площадь S2 + S3 = (13/2)√3*(2/√3) = 13 см².
Ответ: S(KLMN) = 24 - 13 =11 см².