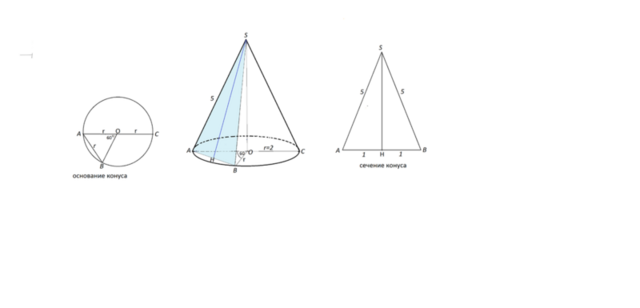
Задача1.
Рассмотрим треугольник МSВ.
В нем SM=SB=AS=AВ,
так как SA и SM равны как образующие, а
АВ - основание равностороннего треугольника SAВ.
Отсюда треугольник МSВ - равнобедренный.
Площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между ними.
S Δ МSВ= 0,5·MS·BS·sin (30°)=0,5 r·r·1/2=0,25 r²
Задача 2.
Сечение ASB данного конуса - равнобедренный треугольник с боковыми сторонами- образующими конуса и основанием АВ, равным радиусу основания конуса, т.к. равнобедренный треугольник АОВ с центральным углом АОВ=60 градусов - равносторонний и АВ=r=2
Площадь ΔАSB=SH·AB:2
SН=√(SА²-АН²)=√(25-1)=2√6
S Δ АSB=2√6·2:2=2√6