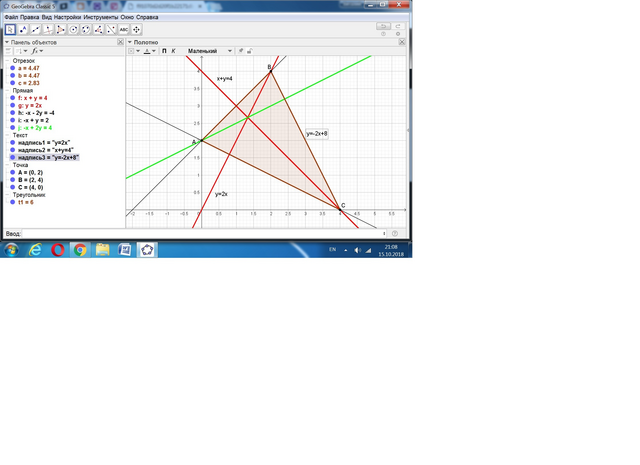
3.09) Дана точка А(0;2) и две высоты х + у = 4 (или у = 4 - х), у = 2х.
Из точки А проводим 2 перпендикуляра АВ и АС к заданным высотам. Это 2 стороны треугольника. Так как точка А находится на оси ординат (у = 2), то у всех прямых, проходящих через эту точку, коэффициент в равен 2.
к(АВ) = -1/к(у=4-х) = -1/(-1) = 1.
Получаем уравнение стороны АВ: у = х + 2.
к(АС) = -1/к(у=2х = -1/(2) = -1/2.
Получаем уравнение стороны АС: у = (-1/2)х + 2.
Находим координаты точек В и С, приравнивая уравнения прямых.
у(АВ) = у(2х).
х + 2 = 2х,
х = 2, у = 2*2 = 4.
Точка В(2; 4).
у(АС) = у(4 - х),
(-1/2)х + 2 = 4 - х,
(1/2)х = 2, х = 2*2 = 4, у = 4 - 4 = 0.
Точка С(4; 0).
Уравнение стороны ВС: В(2; 4), С(4; 0).
ВС: (х - 2)/(4 - 2) = (у - 4)/(0 - 4),
(х - 2)/(2) = (у - 4)/(- 4) это каноническое уравнение.
-4х + 8 = 2у - 8,
2у = -4х + 16,
ВС: у = -2х + 8.
Угловой коэффициент третьей высоты на сторону ВС равен (тоже через точку А):
к3 = -1/к(ВС) = -1/(-2) = 1/2.
у = (1/2)х + 2.