Добрый день!
Чтобы найти все n я предлагаю решать через анализ функций.
Пусть F(n) =  , а G(n) = n(5n+1)
, а G(n) = n(5n+1)
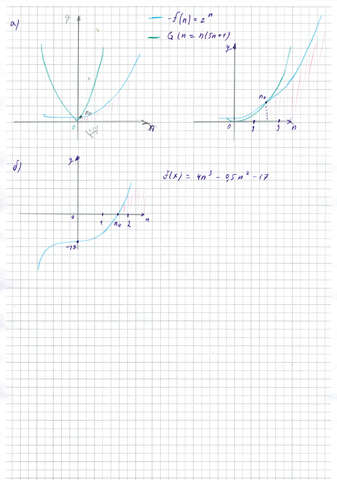
Очевидно, что графиком G(n) является парабола с вершинной в координатах (0;0) а F(n) - кривая степенной функции.
Так как F(n) возрастает быстрее чем G(n), => есть n при котором эти функции будут равны друг другу, но нам не нужно находить это n, так как n - натуральное число, то нам необходимо найти в каком интервале будет находиться n0 при котором F(n) = G(n), другими словами где F(n) станет > G(n)
Как это найти? Ну... конечно можно решать уравнение F(n)-G(n) = 0, но проще и не ошибочно будет сделать прикидку. )
Пусть n = 1 , F(n) = 2 G(n) =6 не уд.
n = 2 4>22 - не уд
n = 5 32 >150 не уд
n = 9 512 > 414 - уд (следовательно диапозон уменьшен с 1 до + бесконечности до [5; 9]
n = 8 256 > 328 - не уд
Таким образом мы выяснили, что n0 находиться в интервале [8; 9] и проверив крайние точки убедились, что при n = 9 F(n)>G(n), следовательно
Ответ: n ∈ [9; +∞)
№2
Аналогично, и даже проще.
Для начала приведём неравенство к виду
4n^3 - 1/2 n^2 -17 >0
Заметим, что графиком будет являться кривая с перегибом в точке с координатами (0; -17) (Это легко понять так как существует свойство для функция 3 степени, что смещение по y зависит от свободного члена уравнения в нашем случае это -17)
Таким образом функция начнёт постепенно возрастать от y = -17 до +∞, но в какой-то момент график функции обязательно пересечёт ось Х, при n0
Но нам опять же не важно при каком конкретном n0 это будет, нам лишь важен интервал в котором это произойдёт.
Пусть n = 1, тогда 4-0,5-17 < 0 - не уд
n = 2 тогда 32 -2-17 > 0
Следовательно функция пересечёт ось Х при n0, где n0 ∈ [1 ; 2]
Таким образом проверяем крайние точки этого интервала (мы их уже проверили выше) и убеждаемся, что при
n∈[2 +∞) функция 4n^3 -1/2 n^2 -17 > 0
Ответ: n∈[2 +∞)
Фото рисунков графиков я прикрепил.