Вот на Ваш суд такой вариант (я его дал в znanija.com/task/820813).
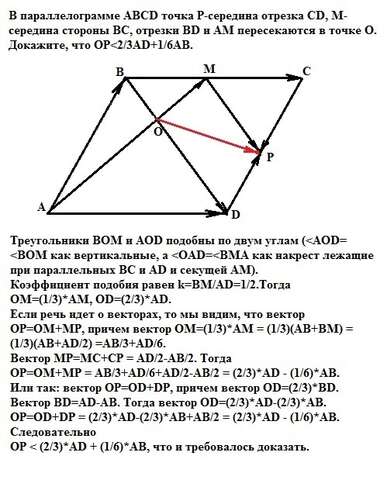
Треугольники ВОМ и AOD подобны по двум углам (
Если речь идет о векторах, то мы видим, что вектор ОР=ОМ+МР, причем вектор ОМ=(1/3)*АМ = (1/3)(АВ+BM) = (1/3)(АВ+AD/2) =AB/3+AD/6. Вектор MP=MC+CP = AD/2-AB/2. Тогда
ОР=ОМ+МР = AB/3+AD/6+AD/2-AB/2 = (2/3)*AD - (1/6)*AB.
Или так: вектор ОР=ОD+DР, причем вектор ОD=(2/3)*BD.
Вектор BD=AD-AB. Тогда вектор OD=(2/3)*AD-(2/3)*AB.
ОР=ОD+DР = (2/3)*AD-(2/3)*AB+AB/2 = (2/3)*AD - (1/6)*AB.
Следовательно
ОР < (2/3)*AD + (1/6)*AB, что и требовалось доказать.