Вычислите площадь фигуры ограниченной линиями :1) y=x^2, 2) y= x+2

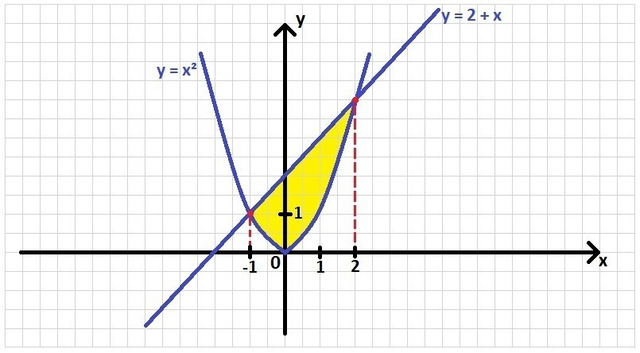
Найти площадь фигуры, ограниченной кривыми.

Для решения задачи в первую очередь нужно построить график.

По графику видно, что найти нам нужно площадь области, лежащей над параболой y = x² и под прямой y = x + 2.

Найдём точки пересечения данных кривых. Для этого нужно решить систему из уравнений их функций.

$\begin{cases}y = x^2,\\y = x + 2;\end{cases}\\\\x^2 = x + 2;\\x^2 - x - 2 = 0;\\D = [b^2 - 4ac] = (-1)^2 - 4\times(-2) = 1 + 8 = 9 = 3^2;\\x_{1,2} = \left[\dfrac{-b\pm\sqrt{D}}{2a}\right] = \dfrac{1\pm 3}{2};\\x_1 = 2, x_2 = -1.$

Найти площадь фигуры, ограниченной сверху графиком функции y = x + 2, а снизу функцией y = x², а так же прямыми x = 2 и x = -1, значит вычислить следующий определённый интеграл.

$\int\limits^{2}_{-1}(x + 2 - x^2) dx = \int\limits^{2}_{-1}x dx + 2\int\limits^{2}_{-1}dx - \int\limits^{2}_{-1}x^2 dx = \dfrac{1}{2}x^2|^{2}_{-1} + 2x|^{2}_{-1} - \dfrac{1}{3}x^3|^{2}_{-1} =\\\\=\dfrac{1}{2}(2^2 - (-1)^2) + 2(2 - (-1)) - \dfrac{1}{3}(2^3 - (-1)^3) = \dfrac{3}{2} + 6 - \dfrac{9}{3} =1,5 + 3 = 4,5.$

Вычислите площадь фигуры ограниченной линиями :1) y=x^2, 2) y= x+2

Найти площадь фигуры, ограниченной кривыми.

Ответ: 4,5.